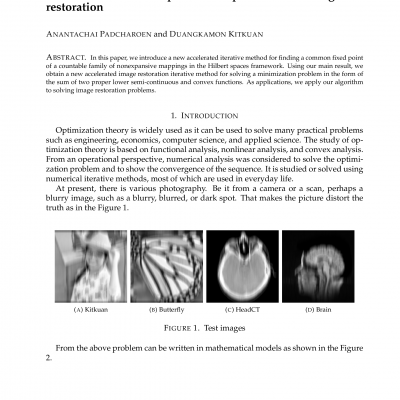
carpathian_2021_37_3_361_380Variational inclusion is an important general problem consisting of many useful problems like variational inequality, minimization problem and nonlinear monotone equations. In this article, a new scheme for solving variational inclusion problem is proposed and the scheme uses inertial and relaxation techniques. Moreover, the scheme is self adaptive, that is, the stepsize does not depend on the factorial constants of the underlying operator, instead it can be computed using a simple updating rule. Weak convergence analysis of the iterates generated by the new scheme is presented under mild conditions. In addition, schemes for solving variational inequality problem and split feasibility problem are derived from the proposed scheme and applied in solving Nash-Cournot equilibrium problem and image restoration. Experiments to illustrate the implementation and potential applicability of the proposed schemes in comparison with some existing schemes in the literature are presented.
