In this work, we prove the Hyers–Ulam stability of hom-derivations in complex Banach algebras, associated with the additive ![]() -functional inequality:
-functional inequality:
(1) 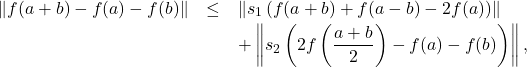
where ![]() and
and ![]() are fixed nonzero complex numbers with
are fixed nonzero complex numbers with ![]() .
.
In this work, we prove the Hyers–Ulam stability of hom-derivations in complex Banach algebras, associated with the additive ![]() -functional inequality:
-functional inequality:
(1) 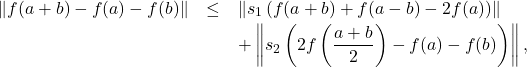
where ![]() and
and ![]() are fixed nonzero complex numbers with
are fixed nonzero complex numbers with ![]() .
.
| Author(s) | Mouktonglang, Thanasak, Suparatulatorn, Raweerote, Park, Choonkil |
|---|---|
| DOI | https://doi.org/10.37193/CJM.2022.03.26 |