carpathian_2021_37_2_161_171Consider in a bounded domain 
, 
, with smooth boundary 
, the following eigenvalue problem
(1) 
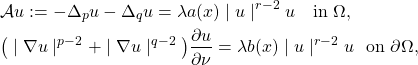
where 
or 
; 
if 
and 
if 
; 
are given nonnegative
functions satisfying
![\[ \int_\Omega a~dx+\int_{\partial\Omega} b~d\sigma >0. \]](https://www.carpathian.cunbm.utcluj.ro/wp-content/ql-cache/quicklatex.com-62495d43be116d11698bb946375f33a3_l3.png "Rendered by QuickLaTeX.com")
Under these assumptions we prove that the set of all eigenvalues of the above problem is the interval 
. Our result complements those previously obtained by Abreu, J. and Madeira, G., [Generalized eigenvalues of the 
Laplacian under a parametric boundary condition, Proc. Edinburgh Math. Soc., 63 (2020), No. 1, 287–303], Barbu, L. and Moroşanu, G., [Full description of the eigenvalue set of the 
-Laplacian with a Steklov-like boundary condition, J. Differential Equations, in press], Barbu, L. and Moroşanu, G., [Eigenvalues of the negative – Laplacian under a Steklov-like boundary condition, Complex Var. Elliptic Equations, 64 (2019), No. 4, 685–700], Fărcăşeanu, M., Mihăilescu, M. and Stancu-Dumitru, D., [On the set of eigen-values of some PDEs with homogeneous Neumann boundary condition, Nonlinear Anal. Theory Methods Appl., 116 (2015), 19–25], Mihăilescu, M., [An eigenvalue problem possesing a continuous family of eigenvalues plus an isolated eigenvale, Commun. Pure Appl. Anal., 10 (2011), 701–708], Mihăilescu, M. and Moroşanu, G., [Eigenvalues of 
under Neumann boundary condition, Canadian Math. Bull., 59 (2016), No. 3, 606–616].
